Mathematical tiles
From the seventeenth century, ‘Mathematical' tiles were used in building, most notably in Sussex and Kent. The origin of the name is unknown. These were tiles with large pegs at the rear which, when nailed onto wooden laths in overlapping layers, resembled brickwork.
The 18th century house was geometrically composed using Palladian principles; where a precise linear grid across the facade was desired, it was usually achieved with ashlar stone or rubbed brickwork. These products were, however, quite expensive so during the Georgian period the technique of hanging ‘mathematical tiles’ was introduced, as a way of imitating high quality bricks. They were produced during the late eighteenth and early nineteenth centuries, in different colours to match the bricks that was in fashion.
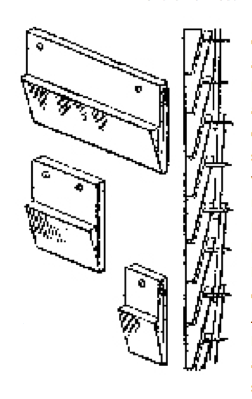
Grey, white and yellow tiles were used in fashionable Brighton and Lewes, whilst black glazed mathematical tiles, in imitation of salt-glazed brickwork, can still be seen as applied to the front elevations of Brighton's Royal Crescent, where developer J. Otto set black glazed mathematical tiles against a light coloured mortar. The colouring was achieved either through the addition of brick dust to the raw clay, or through the use of a liquid slip.
Mathematical tiles became very fashionable in their own right, many medieval buildings being refaced with them, while they had the added advantage of providing excellent protection from the elements.
The tiles were moulded with a lip on the reverse side enabling them to be fitted against battens in much the same way as roofing tiles, although they were sometimes bedded into mortar. Since mathematical tiles were unable to encompass right angles the corners of mathematically tiled houses were usually fitted with a painted board in order to finish the tile courses neatly. Batty Langley, writing in the 18th century, described mathematical tile facades as “most beautiful” with only the returns of the wall “betraying the trick”.
While the tile surface is never as uniformly flat as that of a brick wall, the reflection of light on the tiles produces an attractive effect.